1.什么是伯特兰德模型
2.伯特兰德模型的前提假定
| 经济分析工具 |
|---|
| [编辑] |
伯特兰德模型假定,当企业制定其价格时,认为其他企业的价格不会因它的决策而改变,并且n个(为简化,取n=2)寡头企业的产品是完全替代品。A、B两个企业的价格分别为P1、P2 ,边际成本都等于C。
3.伯特兰德模型存在的问题
4.对伯川德模型的评价
伯川德模型假设价格为策略性变量而更为现实,但是它所推导出的结果却过于极端;但由于与现实不甚相符而遭到了很多学者的批评。这是我们为什么将其称之为伯川德悖论的主要原因。因此,学者们在研究市场中企业的竞争行为时,更多的是采用古诺模型,即用产量作为企业竞争的决策变量。
5.伯特兰德模型的相关案例[1]
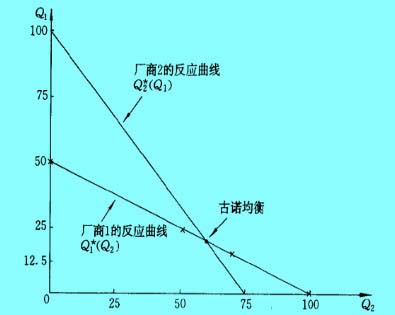
- 图1反应曲线与古诺均衡
假设双寡头面临如下一条线性需求曲线:
P=30-Q
其中,Q为两厂商的总产量,即Q=Q1+Q2。
再假设边际成本为零,即:
MCl=MC2=0
厂商l的总收益TR1由下式给出:
TR1=PQ1=(30一Q)Ql=30Ql-(Q1)2-Q1Q2
厂商l的边际收益MR1为:
MRl=30—2Q-Q2
利用利润最大化条件MRl=MCl=0,得厂商l的反应函数(reaction function)为:
Ql=15—0.5Q2 (1—1)
同理可得厂商2的反应曲线为:
Q2=15-0.5Ql (1—2)
均衡产量水平就是两个反应曲线交点Q1和Q2的值,即方程组(1—1)式和(1—2)式的解,我们可以求得古诺均衡时的均衡产量水平为:Ql=Q2=10。如图2所示。
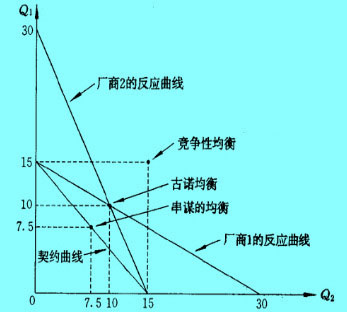
- 图2双寡头的均衡
因此,在本例中,两个寡头的总产量Q为Q1+Q2=20,均衡价格为p=30-Q=10。
刚才我们讨论了两寡头厂商相互竞争时的均衡产量。现在我们放宽不能串谋的假设,假定两寡头可以串谋,它们能共同确定产量以使总利润最大化。
这时,两厂商的总收益TR为:
TR=PQ=(30一Q)Q=30Q—Q2
其边际收益MR为:
MR=30—2Q
根据利润最大化条件MR=MC=0,可以求得当Q=15时总利润最大。如果两厂商同意平分利润,每个寡头厂商将各生产总产量的一半,即Q1=Q2=7.5。其实,任何相加为15的产量Ql和Q2的组合都使总利润最大化,因此,把Q1+Q2=15称为契约曲线,而Ql=Q2=7.5是契约曲线上的一个点。如图2所示。
我们还可以求得当价格等于边际成本时,Q1=Q2=15,各厂商的利润为零。
从3个均衡产量可以看到,竞争性均衡时,厂商价格最低,产量最高,利润为零;串谋均衡时,厂商价格最高,产量最低,利润最高。
古诺模型和斯塔克尔伯格模型都是把厂商的产量作为竞争手段,是一种产量竞争模型,而伯特兰德模型是价格竞争模型。在这种模型中,各寡头厂商通过选择价格进行竞争,而且各寡头厂商生产的产品是同质的,寡头厂商之间也没有正式或非正式的串谋行为。这一模型是由法国经济学家约瑟夫·伯特兰德(Joseph Bertrand)于1883年建立的。现在我们继续使用上例的数据。设两个寡头构成的总市场需求曲线为:
P=30-Q其中Q=Q1+Q2,与上例不同的是,现在两个厂商有相同的、不为零的边际成本,譬如:MC1=MC2=3
当两个寡头厂商同时选择产量时,利用上述古诺模型求解均衡产量的方法可以求得古诺均衡是Q1=Q2=9,此时的市场价格为12元,每个厂商均获利8l元。
不过,现在我们要确定的不是同时选择产量时的均衡,而是双方通过同时选择价格竞争时的均衡状态。由于产品是同质的,消费者将只会从低价格的厂商处购买。一旦两个寡头定价不同,定高价的厂商将不能出售任何产品,而定低价的厂商则占据整个市场。因此这种情况将不会出现,这意味着两寡头厂商将定相同的价格,这样对消费者来说,从哪个厂商购货都是无差别的。但是,最后具体的价格又是多少呢?现在假设两个厂商竞争的结果是价格都是高于3元的某个值,那么在这种情况下,任何一个厂商稍微降价它就将占领整个市场而另一个厂商将丧失所有的客户;如果两个厂商竞争的结果是价格都低于3元的某个值,那么双方都会亏损。只有当双方的价格都等于边际成本3元时(P1=P2=3),双方再也没有改变这一价格的动力,此时市场的总产量为27个单位,假如双方各供给市场一半,即每个厂商都生产13.5个单位,则双方都没有利润。在博弈论中,这种状态称为纳什(Nash)均衡。这里的纳什均衡也是一种完全竞争的均衡:厂商产量由边际成本等于边际收益等于价格来确定,每个厂商的利润为零。
把伯特兰德模型的完全竞争均衡状态与古诺模型的古诺均衡状态相比可以发现,当把竞争策略选择变量从古诺模型的产量改为伯特兰德模型的价格时,每个厂商的产量从9单位增加到13.5单位,价格从12元降低为3元,利润从81元降为零。