古诺模型又称古诺双寡头模型（Cournot duopoly model），或双寡头模型（Duopoly model）,古诺模型是早期的寡头模型。它是由法国经济学家古诺于1838年提出的。是纳什均衡应用的最早版本，古诺模型通常被作为寡头理论分析的出发点。古诺模型是一个只有两个寡头厂商的简单模型，该模型也被称为“双头模型”。古诺模型的结论可以很容易地推广到三个或三个以上的寡头厂商的情况中去。

古诺模型假定一种产品市场只有两个卖者，并且相互间没有任何勾结行为，但相互间都知道对方将怎样行动，从而各自怎样确定最优的产量来实现利润最大化，因此，古诺模型又称为双头垄断理论。

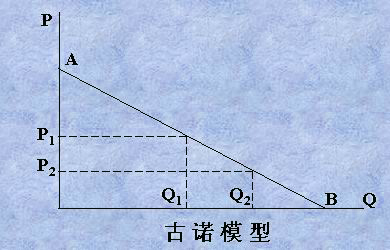^[1]

经济分析工具
埃奇沃斯盒状图 埃奇沃斯模型 伯特兰德模型 巴斯塔布尔标准 纯生产率效应 彩票选择实验 ELES模型 方差比率检验 古诺模型 国际卡特尔 霍特林模型 货币先行模型 价格领导模型 价格卡特尔 均衡分析法 经济系统工程 经济控制论模型 卡特尔模型 肯普标准 穆勒标准 偏好诱导实验 70规则 斯威齐模型 斯塔克尔伯格模型 萨缪尔森经济学方法论 社会核算矩阵 讨价还价模型 消费者剩余 希尔施模型 演化经济学方法论 滞后变量模型 自动估值模型
[编辑]

A厂商的均衡产量为：

OQ（1/2―1/8―1/32―……）=1/3 OQ

B厂商的均衡产量为：OQ（1/4+1/16+1/64+……）=1/3 OQ

行业的均衡总产量为：1/3 OQ+1/3 OQ=2/3 OQ

以上双头古诺模型的结论可以推广。令寡头厂商的数量为m，则可以得到一般的结论如下：

每个寡头厂商的均衡产量=市场总容量/（m+1）

行业的均衡总产量=市场总容量·m/（m+1）

古诺模型的缺陷是假定了厂商以竞争对手不改变产量为条件。