市场调查方法
A 案头调研 案例研究法 B 不重复抽样 C 抽样调查 重置抽样 抽签法 产品留置测试 D 多维尺度法 定量研究方法 定性研究方法 典型调查法 电话调查 多阶段抽样 等距抽样 独立控制配额抽样 等距量表 等比量表 E 二手资料调研 二路焦点小组 F 非概率抽样 分层抽样 分层比例抽样 分层最佳抽样 G 观察法 概率抽样 拐点调研 滚雪球抽样 H 会议调查 J 焦点访谈法 经验判断法 随机抽样 家庭日记法 经销商访谈 K 可行性研究 控制实验法 L 联合分析法 留置调查 垃圾调研法 类别量表 M 面谈访问法 盲测 描述性调研 媒介调查法 P PPS 判断抽样 配额抽样 平衡量表法 评价量表 配对比较量表 Q Q分类法 R 任意抽样 S 容量测定法 SEM模型 深层访谈法 双重抽样 实验调查法 实地调研 数值分配量表 随机号码表法 顺序量表 T 投影技法 推销估计法 投射研究 探索性调研 W 文献调查法 问卷调查法 网络调研 文案调查法 无准备访问 网上调查 X 询问法 辛迪加调研 行踪分析 相互控制配额抽样 Y 邮寄调查 因果性调研 Z 主观概率法 整群抽样 重点调查 逐户寻找法
[编辑]

在配对比较量表中，受测者被要求对一系列对象两两进行比较，根据某个标准在两个被比较中的对象中做出选择。配对比较量表也是一种使用很普遍的态度测量方法。它实际上是一种特殊的等级量表，不过要求排序的是两个对象，而不是多个。

配对比较方法克服了等级排序量表存在的缺点。首先，对受测者来说，从一对对象中选出一个肯定比从一大组对象中选出一个更容易；其次，配对比较也可以避免等级量表的顺序误差。但是，因为一般要对所有的配对进行比较，所以对于有n个对象的情况，要进行n(n-1)/2次配对比较，是关于n的一个几何级数。因此，被测量的对象的个数不宜太多，以免使受测者产生厌烦而影响应答的质量。

下面的表1是一个配对比较量表的例子。

访问结束之后，可以将受测者的回答整理成表格的形式，下面的表2是根据某受访者的回答整理得到的结果。表中每一行列交叉点上元素表示该行的品牌与该列的品牌进行比较的结果，其中元素“1”表示受测者更喜欢这一列的品牌，“0”表示更喜欢这一行的品牌。将各列取值进行加总，得到表中合计栏，这表明各列的品牌比其它品牌更受偏爱的次数。

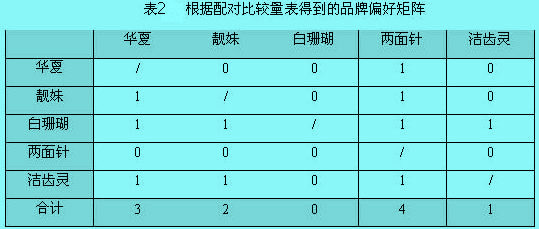
从上表中看到该受测者在华夏牙膏和靓妹牙膏中更偏爱前者（第二行第一列数字为1）。在“可传递性”的假设下，可将配对比较的数据转换成等级顺序。所谓“可传递性”是指，如果一个人喜欢A品牌甚于B品牌，喜欢B品牌甚于C品牌，那么他一定喜欢A品牌甚于C品。将表的各列数字分别加总，计算出每个品牌比其他品牌更受偏爱的次数，就得到该受测者对于5个牙膏品牌的偏好，从最喜欢到最不喜欢，依次是两面针、华夏、靓妹、洁齿灵和白珊瑚。假设调查样本容量为100人，将每个人的回答结果进行汇总，将得到表3的次数矩阵。再将次数矩阵变换成比例矩阵（用次数除以样本数），如表3所示，在品牌自身进行比较时，我们令其比例为0.5。

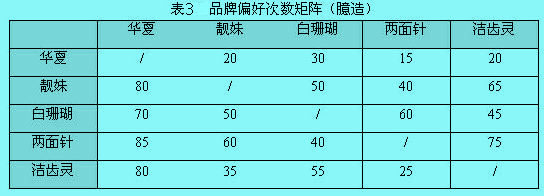
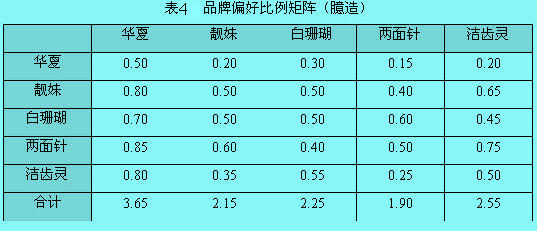
从表4中的合计栏中，可以看出5个品牌中华夏牌牙膏被认为是最好的，洁齿灵次之，再次是白珊瑚和靓妹，两面针最差。但这是一个顺序量表，只能比较各品牌的相对位置，不能认为“华夏牙膏比洁齿灵要好1.1，白珊瑚要比靓妹好0.1”。要想衡量各品牌偏好间的差异程度必须先将其转化为等距量表，这里就不再深入讨论了。

当要评价的对象的个数不多时，配对比较法是有用的。但如果要评价的对象超过10个，这种方法就太麻烦了。另外一个缺点是“可传递性”的假设可能不成立，在实际研究中这种情况常常发生。同时对象列举的顺序可能影响受测者，造成顺序反应误差。而且这种“二中选一”的方式和实际生活中作购买选择的情况也不太相同，受访者可能在A、B两种品牌中对A要略为偏爱些，但实际上却两个品牌都不喜欢。