1.什么是连锁店悖论
2.连锁店悖论的论证过程[1]
莱茵哈德·泽尔腾(1978)提供了一个典型的博弈,它明确了排除掠夺性定价成为均衡现象所必须具备的信息方面的严格条件。他设想一家主导企业(即现有企业)在20个不同的地区市场内经营连锁店。在每个市场,它都面临单个竞争对手的进入可能。
下图显示了一期博弈的博弈树和收益矩阵。其中,每个进入者得到的收益由单个市场决定,现有企业的总收益则是20个市场内所有连锁店的收益之和。
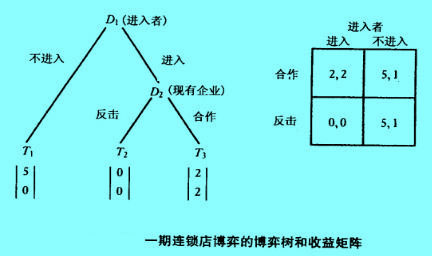
在每个市场,进人者的选择是进入还是不进入市场。如果进入者不进入市场,那么,它得到的收益便是1欧元(另一最佳投资的收益),而现有企业得5欧元。如果进入者进入市场,那么,现有企业就必须决定是与进入者合作(双方都得2欧元),还是反击进人者(双方都得到零收益)。选择合作的现有企业将限制产量并与进入者分享市场,而选择反击的现有企业即使以利润损失为代价,也要扩大产量。塞尔顿比较了现有企业的两种可能策略。其中阻止策略是基于这样的事实,即如果进入者相信现有企业会积极反击,那么,进入者还是以不进入市场的为好。根据这一观点,现有企业最佳的策略是宣布要对进入者进行积极的反击。如果进入发生,那么,其有可能发生在早期,这样,现有企业必须牺牲自己的利润以实施阻止进入的威胁。但如果后来的潜在进入者相信现有企业积极反击进入的威胁是当真的,那么,现有企业最终会有盈手0。塞尔顿指出阻止策略在最后的市场是不起作用的。
在最后一期积极反击意味着现有企业有损失但以后却没有收益了,因此,在最后的市场里积极反击的威胁显然是空的。一家有意进人倒数第二期市场的聪明的企业会进行后向归纳,并得出结论:既然追求最大化收益的现有企业在最后一期的积极反击不会有收益,那么,它在倒数第二期的积极反击也不会有收益。假设现有企业在前三个市场内对进人采取积极反击的策略,并且直到最后三期市场以前都没有进入发生。由于意识到博弈将要结束,或基本将要结束了,现有企业会在最后三期市场内允许进人。这样,它的收益便是76欧元(3×0+14×5+3×2)。后向归纳观点的逻辑结论,是建立在现有企业在最后一期积极反击的威胁不可信的基础之上的。即如果现有企业在最后一期阻止进入的威胁不可信,那么,它在倒数第二期对进入采取积极反击就不会有收益。但在这种情况下,它在第18期对进入采取积极反击也不能获得收益,如此可一直推理到第l期。这样,每一期的进入者都不会相信现有企业积极反击的威胁,惟一的子博弈完美均衡是进入者在每期都进人且现有企业在每期都允许进入,这样,现有企业的收益将是40欧元。
尔顿对他的讨论作了如下总结:在博弈论上,只有归纳理论才是正确的。从逻辑上讲,归纳观点不能被限制在博弈的最后几期。一个不可避免的结论是,归纳观点应被应用到博弈的所有阶段。但是,阻止理论更令人信服。如果我必须参加博弈并且是博弈中的(现有企业),那我就会遵循阻止理论。如果阻止理论行不通,我会感到非常惊讶。从我与朋友和同事的讨论中,我得到的印象是大多数人都抱有同样的态度……我的经验显示,受过数学训练的人会认识到归纳观点的逻辑正确性,但他们却拒绝把它作为实际行为的指导。似乎可以推测,即使在所有博弈者都知道所有博弈者都十分透彻地理解了归纳观点的情况下,(现有企业)还是会采取阻止策略,并且其他博弈者对它的预期也是这样做。归纳理论的逻辑必然性并不能推翻貌似有理的阻止理论这一事实,这是一个严重的问题,它可以被称为是一个悖论。