风险分析有狭义和广义两种，狭义的风险分析是指通过定量分析的方法给出完成任务所需的费用、进度、性能三个随机变量的可实现值的概率分布。而广义的风险分析则是一种识别和测算风险，开发、选择和管理方案来解决这些风险的有组织的手段。它包括风险识别、风险评估和风险管理三方面的内容。本文中论及风险分析时，都采用后一种定义。

风险识别是指确定哪些可能导致费用超支、进度推迟或性能降低的潜在问题，并定性分析其后果。在这一步须作的工作是分析系统的技术薄弱环节及不确定性较大之处，得出系统的风险源，并将这些风险源组合成一格式文件供以后的分析参考。它属于定性分析的范围。风险评估是指对潜在问题可能导致的风险及其后果实行量化，并确定其严重程度。这其中可能牵涉到多种模型的综合应用，最后得到系统风险的综合印象。而风险管理则是指在风险识别及风险分析的基础上采取各种措施来减小风险及对风险实施监控。这也可以说是风险分析的最终目的。

风险分析是对风险影响和后果进行评价和估量，包括定性分析和定量分析。其中，定性分析是评估已识别风险的影响和可能性的过程，按风险对项目目标可能的影响进行排序。其作用和目的为：识别具体风险和指导风险应对；根据各风险对项目目标的潜在影响对风险进行排序；通过比较风险值（Risk Scores）确定项目总体风险级别（Overall Risk Ranking for teh Project）。定量分析是量化分析每一风险的概率及其对项目目标造成的后果，也分析项目总体风险的程度。其作用和目的为：测定实现某一特定项目目标的概率；通过量化各个风险对项目目标的影响程度，甄别出最需要关注的风险；识别现实的和可实现的成本、进度及范围目标。

1.风险识别

风险因素识别应注意借鉴历史经验，特别是后评价的经验。同时可运用“逆向思维”方法来审视项目，寻找可能导致项目“不可行”的因素，以充分揭示项目的风险来源。

风险识别要根据行业和项目的特点，采用分析和分解原则，把综合性的风险问题分解为多层次的风险因素。

常用的方法主要有风险分解法、流程图法、头脑风暴法和情景分析法等。具体操作中，大多通过专家调查的方式完成。

2.风险估计

风险估计：估计风险发生的可能性及其对项目的影响。应采取定性描述与定量分析相结合的方法对风险做出全面估计。

注意：定性与定量不是绝对的，在深入研究和分解后，有些定性因素可以转化为定量因素。

风险估计的方法如下图所示。

3.风险评价

风险评价：是在风险估计的基础上，通过相应的指标体系和评价标准，对风险程度进行划分，以揭示影响项目成败的关键风险因素。风险评价包括单因素风险评价和整体风险评价。

(1)单因素风险评价，即评价单个风险因素对项目的影响程度，以找出影响项目的关键风险因素。评价方法主要有风险概率矩阵、专家评价法等。

(2)项目整体风险评价，即综合评价若干主要风险因素对项目整体的影响程度。对于重大投资项目或估计风险很大的项目，应进行投资项目整体风险分析。

4.风险对策

风险对策研究的作用：

(1)在投资项目决策前的可行性研究中，不仅要了解项目可能面临的风险，且要提出针对性的风险对策，避免风险的发生或将风险损失减低到最小程度，才能有助于提高投资的安全性，促使项目获得成功。

(2)同时，可行性研究阶段的风险对策研究可为投资项目实施过程的风险监督与管理提供依据。

(3)另外，风险对策研究的结果应及时反馈到可行性研究的各个方面，并据此修改部分数据或调整方案，进行项目方案的再设计。

可行性研究阶段的风险对策研究是整个项目风险管理的重要组成部分，对策研究的基本要求包括：

(1)风险对策研究应贯穿于可行性研究的全过程。

(2)风险对策应具针对性。针对特定项目主要的或关键的风险因素提出必要的措施，将其影响降低到最小程度。

(3)风险对策应有可行性。所谓可行，不仅指技术上可行，且从财力、人力和物力方面也是可行的。

(4)风险对策必具经济性。在风险对策研究中应将规避防范风险措施所付出的代价与该风险可能造成的损失进行权衡，旨在寻求以最少的费用获取最大的风险效益。

(5)风险对策研究是项目有关各方的共同任务。风险对策研究不仅有助于避免决策失误而且是投资项目以后风险管理的基础，因此它应是投资项目有关各方的共同任务。

5.风险分析结论

完成风险识别和评估后，应归纳和综述项目的主要风险，说明其原因、程度和可能造成的后果，以全面、清晰地展现项目的主要风险。同时将风险对策研究结果进行汇总，教材404页表。

风险分析：认识项目可能存在的潜在风险因素，估计这些因素发生的可能性及由此造成的影响，分析为防止或减少不利影响而采取对策的一系列活动。

它包括风险识别、风险估计、风险评价与对策研究四个基本阶段。

项目决策分析中的风险分析应遵循以下程序：

首先从认识风险特征入手去识别风险因素;然后选择适当的方法估计风险发生的可能性及其影响;

其次，评价风险程度，包括单个风险因素风险程度估计和对项目整体风险程度估计;

最后，提出针对性的风险对策，将项目风险进行归纳，提出风险分析结论。

1.风险函数

描述风险有两个变量。一是事件发生的概率或可能性(Probability)，二是事件发生后对项目目标的影响(Impact)。风险可以用一个二元函数描述：

R (p，I)=p×I

其中：p为风险事件发生的概率;I为风险事件对项目目标的影响。

风险的大小或高低既与风险事件发生的概率成正比，也与风险事件对项目目标的影响程度成正比。

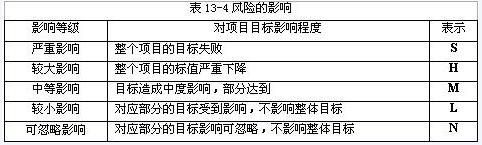
2.风险影响

按照风险发生后对项目的影响大小，可以划分为五个影响等级。如下表13-4所示：

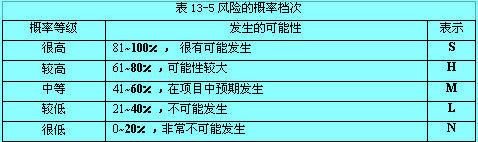
3.风险概率

按照风险因素发生的可能性，可以将风险概率划分为五个档次如下表13-5所示：

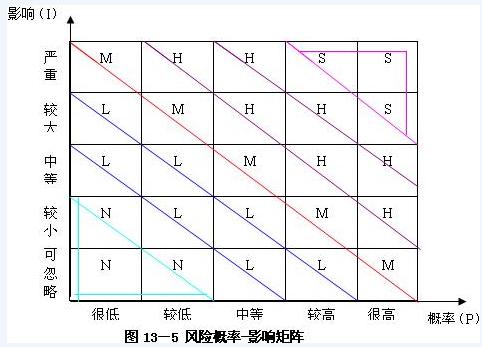
4.风险评价矩阵(PIM)

风险的大小可以用风险评价矩阵，也称概率-影响矩阵来表示。它以风险因素发生的概率为横坐标，以风险因素发生后对项目的影响大小为纵坐标，如图13-5。

5.风险等级

一、风险综合评价法

风险综合评价的方法中，最常用、最简单的分析方法是通过调查专家的意见，获得风险因素的权重和发生概率，进而获得项目的整体风险程度。其步骤主要包括：

1.建立风险调查表。在风险识别完成后，建立投资项目主要风险清单，将该投资项目可能遇到的所有重要风险全部列入表中。

2.判断风险权重。

3.确定每个风险发生概率。可以采用1-5标度，分别表示可能性很小、较小、中等、较大、很大，代表5种程度。

4.计算每个风险因素的等级。

5.最后将风险调查表中全部风险因素的等级相加，得出整个项目的综合风险等级。

二、蒙特卡洛模拟

1.使用条件：

当在项目评价中输入的随机变量个数多于三个，每个输入变量可能出现三个以上以至无限多种状态时(如连续随机变量)，就不能用理论计算法进行风险分析，这时就必须采用蒙特卡洛模拟技术。

2.原理

用随机抽样的方法抽取一组输入变量的数值，并根据这组输入变量的数值计算项目评价指标，抽样计算足够多的次数可获得评价指标的概率分布，并计算出累计概率分布、期望值、方差、标准差，计算项目由可行转变为不可行的概率，从而估计项目投资所承担的风险。

3.蒙特卡洛模拟的程序

①确定风险分析所采用的评价指标，如净现值、内部收益率等。

②确定对项目评价指标有重要影响的输入变量。

③经调查确定输入变量的概率分布。

④为各输入变量独立抽取随机数。

⑤由抽得的随机数转化为各输入变量的抽样值。

⑥根据抽得的各输入随机变量的抽样值组成一组项目评价基础数据。

⑦根据抽样值组成基础数据计算出评价指标值。

⑧重复第四步到第七步，直至预定模拟次数。

⑨整理模拟结果所得评价指标的期望值、方差、标准差和期望值的概率分布，绘制累计概率图。

⑩计算项目由可行转变为不可行的概率。

4.应用蒙特卡洛模拟法时应注意的问题

(1)在运用蒙特卡洛模拟法时，假设输入变量之间是相互独立的，在风险分析中会遇到输入变量的分解程度问题。

输入变量分解得越细，输入变量个数也就越多，模拟结果的可靠性也就越高。变量分解过细往往造成变量之间有相关性，就可能导致错误的结论。为避免此问题，可采用以下办法处理。

①限制输入变量的分解程度。

②限制不确定变量个数。模拟中只选取对评价指标有重大影响的关键变量，其他变量保持在期望值上。

③进一步搜集有关信息，确定变量之间的相关性，建立函数关系。

(2)蒙特卡洛法的模拟次数。

从理论上讲，模拟次数越多越正确，但实际上一般应在200~500次之间为宜。

三、专家调查法

专家调查法是基于专家的知识、经验和直觉，发现项目潜在风险的分析方法。

适用范围：它适用于风险分析的全过程。

注意：采用专家调查法时，专家应有合理的规模，人数一般应在10-20位左右。专家的人数取决于项目的特点、规模、复杂程度和风险的性质而定，没有绝对规定。

专家调查法有很多，其中头脑风暴法、德尔菲法、风险识别调查表、风险对照检查表和风险评价表是最常用的几种方法。

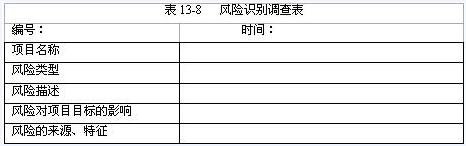
1.风险识别调查表

主要定性描述风险的来源与类型、风险特征、对项目目标的影响等。

2.风险对照检查表

是一种规范化的定性风险分析工具，具有系统、全面、简单、快捷、高效等优点，容易集中专家的智慧和意见，不容易遗漏主要风险;对风险分析人员有启发思路、开拓思路的作用。

适用范围：

(1)当有丰富的经验和充分的专业技能时，项目风险识别相对简单，并可以取得良好的效果。

(2)对照检查表的设计和确定是建立在众多类似项目经验基础上的，需要大量类似项目的数据。而对于新的项目或完全不同环境下的项目，则难以适应。

需要针对项目的类型和特点，制定专门的风险对照检查表。

3.风险评价表

通过专家凭借经验独立对各类风险因素的风险程度进行评价，最后将各位专家的意见归集起来。风险评价表通常重在说明。

注意：说明中应对程度判定的理由进行描述，并尽可能明确最悲观值(或最悲观情况)及其发生的可能性。

四、风险概率估计

　1.客观概率估计

客观概率：是实际发生的概率，可以根据历史统计数据或是大量的试验来推定。两种方法：

(1)将一个事件分解为若干子事件，通过计算子事件的概率来获得主要事件的概率;

(2)通过足够量的试验，统计出事件的概率。

客观概率估计：是指应用客观概率对项目风险进行的估计，它利用同一事件，或是类似事件的数据资料，计算出客观概率。

客观概率估计法最大的缺点是需要足够的信息，但通常是不可得的。

注意：客观概率只能用于完全可重复事件，因而并不适用于大部分现实事件。

2.主观概率估计

主观概率：基于个人经验、预感或直觉而估算出来的概率，是一种个人的主观判断。

主观概率估计：基于经验、知识或类似事件比较的专家推断概率。

注意：当有效统计数据不足或是不可能进行试验时，主观概率是唯一选择。

主观概率专家估计的具体步骤:

(1)根据需要调查问题的性质组成专家组。专家组成员由熟悉该风险因素的现状和发展趋势的专家、有经验的工作人员组成。

(2)查某一变量可能出现的状态数或状态范围和各种状态出现的概率或变量发生在状态范围内的概率，由每个专家独立使用书面形式反映出来。

(3)整理专家组成员意见，计算专家意见的期望值和意见分歧情况，反馈给专家组。

(4)专家组讨论并分析意见分歧的原因。重新独立填写变量可能出现的状态或状态范围和各种状态出现的概率或变量发生在状态范围内的概率，如此重复进行，直至专家意见分歧程度满足要求值为止。这个过程最多经历三个循环，否则不利于获得专家们的真实意见。

3.风险概率分布

(1)离散型概率分布。输入变量可能值是有限个数。各种状态的概率取值之和等于1，它适用于变量取值个数不多的输入变量。

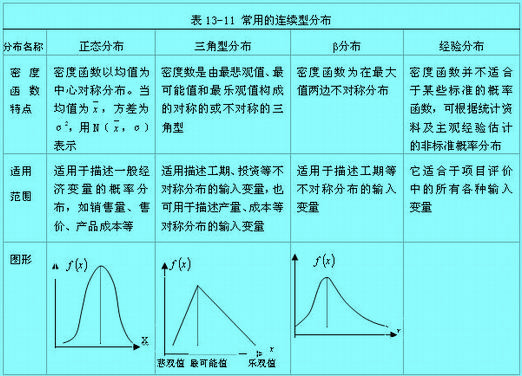
(2)连续型概率分布，输入变量的取值充满一个区间。常用的连续概率分布如下表13-11所示：

4.风险概率分析指标

描述风险概率分布的指标主要有期望值、方差、标准差、离散系数等。

(1)期望值

期望值是风险变量的加权平均值。

②连续型风险变量，期望值为(补充)

(2)方差和标准差

方差和标准差都是是描述风险变量偏离期望值程度的绝对指标。

(3)离散系数

离散系数是一组数据的标准差与其相应的均值之比，是测度数据离散程度的相对指标，其作用主要是用于比较不同组别数据的离散程度。

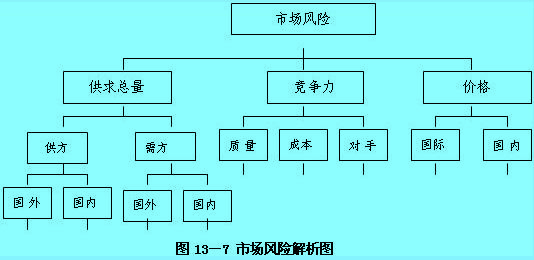
五、风险解析法(RBS Risk Breakdown Structure)

风险解析法，也称风险结构分解法,它将一个复杂系统分解为若干子系统，通过对子系统的分析进而把握整个系统的特征。

六、概率树分析

概率树分析是假定风险变量之间是相互独立的，在构造概率树的基础上，将每个风险变量的各种状态取值组合计算，分别计算每种组合状态下的评价指标值及相应的概率，得到评价指标的概率分布，并统计出评价指标低于或高于基准值的累计概率，计算评价指标的期望值、方差、标准差和离散系数。可以绘制以评价指标为横轴，累计概率为纵轴的累计 概率曲线。

概率树计算项目净现值的期望值和净现值大于或等于零的累计概率的计算步骤：

1)通过敏感性分析，确定风险变量；

2)判断风险变量可能发生的情况；

3)确定每种情况可能发生的概率，每种情况发生的概率之和必须等于1；

4)求出可能发生事件的净现值、加权净现值，然后求出净现值的期望值；

5)可用插入法求出净现值大于或等于零的累计概率。

七、层次分析法

层次分析法(The Analytic Hierarchy Process)是美国著名运筹学家，匹兹堡大学教授T.L Saaty于20世纪70年代中期提出的一种定性与定量相结合的决策分析方法，简称AHP方法。

层次分析法是一种多准则决策分析方法，在风险分析中它有两种用途：一是将风险因素逐层分解识别，直至最基本的风险因素，也称正向分解；二是两两比较同一层次风险因素的重要程度，列出该层风险因素的判断矩阵(判断矩阵可由专家调查法得出)，判断矩阵的特征根就是该层次各个风险因素的权重，利用权重与同层次风险因素概率分布的组合，求得上一层风险的概率分布，直至求出总目标的概率分布，也称反向合成。

运用层次分析法解决实际问题一般包括四个步骤： 1)建立所研究问题的递阶层次结构； 2)构造两两比较判断矩阵； 3)由判断矩阵计算被比较元素的相对权重； 4)计算各层元素的组合权重； 5)将各子项的权重与子项的风险概率分布加权叠加，即得出项目的经济风 险概率分布。