约翰逊法是作业排序中的一种排序方法。选出最短加工时间i*，若最短加工时间有多个，任选1个.若i*出现在机床1，它对应的工件先安排加工，否则放在最后安排，安排后划去该工件,重复上两个步骤，直到所有工件都排序完毕。

约翰逊法适用的条件是：n个工件经过二、三台设备（有限台设备）加工，所有工件在有限设备上加工的次序相同。

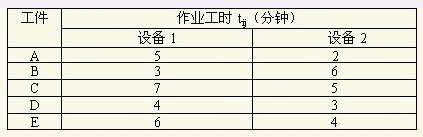
举例说明:有五个工件在二台设备上加工，加工顺序相同，现在设备1上加工，再在设备2上加工，工时列于下表1中，用约翰逊法排序。

表1 加工工时表

第一步，取出最小工时t12=2。如该工时为第一工序的，则最先加工；反之，则放在最后加工。此例是A工件第二工序时间，按规则排在最后加工。

第二步，将该已排序工作划去。

第三步，对余下的工作重复上述排序步骤，直至完毕。此时t21=t42=3，B工件第一工序时间最短，最先加工；D工件第二工序时间最短，排在余下的工件中最后加工。最后得到的排序为：B-C-E-D-A。整批工件的停留时间为27分钟。

这是一种适用于n/2/P/F_max排序问题的静态排序方法约翰逊法的目标是要求得到全组的零件具有最短的生产周期的生产进度表。数学上可以证明，应用约翰逊法所得的排序结果是最优解。

1.约翰逊法的排列规则

如果满足mint_1k;t_2k < mint_2k;t_1k

则将k工件排在h工件之前。

式中：t_1k、t_2k：k工件第1工序、第2工序的加工时间；

t_2k、t_1k：h工件第2工序、第1工序的加工时间。

2.约翰逊排序法的进行步骤

(1)列出零件组的工序矩阵；

(2)在工序矩阵中选出加工时间最短的工序。如果改工序属于第1工序，则将该工序所属工件排在前面。反之，最小工序是第2工序，则将该工序所属的工件排在最后面。若最小的工序又多个，可任选其中的一个；

(3)将已排序的工件从工序矩阵中消去；

(4)继续按步骤(1)、(2)、(3)进行排序，若所有工件都已排定投产顺序，排序即告结束。

例：有6中零件，其工序矩阵见表

表：零件的工序矩阵

工件号	1	2	3	4	5	6
第1工序M1	6	2	9	4	4	5
第2工序M2	8	3	3	5	8	4

根据约翰逊法的排序步骤：

(1)按前工序最小的选出2号工件及后工序最小的选出3号工件前，3号排在后。从原工件矩阵中消去2号及3号零件，见下表。

项目	新工序矩阵		原工序矩阵
工件号	2	3	1	4	5	5
第1工序M1	2	9	6	4	4	5
第2工序M2	3	3	8	5	8	4

(2)对原工件矩阵继续步骤(1)、(2)、(3)，前工序最小的有4和5号两工件可任选其一，后工序最小的为6号工件。选出该两工件，并按前述规则排列，插入新工序矩阵见下表。

项目	新工序矩阵				原工序矩阵
工件号	2	4	6	3	1	5
第1工序M1	2	4	5	9	6	4
第2工序M2	3	5	4	3	8	8

(3)按规则继续进行排序，5号工件排在前，1号工件拍在后。

工序矩阵。表是按约翰逊法排序后的新工艺矩阵。

按约翰逊法排序后的新工艺矩阵

项目	新工序矩阵
工件号	2	4	5	1	6	3
第1工序M1	2	4	6	5	9
第2工序M2	3	5	8	8	4	3

对于同顺序排序问题，可以通过表上作业，计算全组零件的最大流程时间F_max见表

最大流程时间F_max计算表

工件号	2	5	4	1	6	3
第1工序M1	2/2	4/6	4/10	6/16	5/21	9/30
第2工序M2	3/5	5/11	8/19	8/27	4/31	3/34

表中斜线右方的数字是到该工序结束时的流程时间，它的计算方法如下：

到该工序结束时间的流程时间=该工序的开始时间+该工序的加工时间

在生产过程中一个工序的开始时间取决于两个因素：

• 该工序前一道工序的结束时间；

• 该工序所用的设备上紧前工件的加工结束时间。该工序的开始时间应取上述两数中之大者。例如，1号工件第2工件结束时的流程时间，应为F_j1m2=max{16;19}+8=27。

根据上表中的数据可得到一张1至6号工件的生产进度表，有每个工件在各台设备上的开工时间与完工时间。

本例中第4和第5号工件在被选时，由于前工序均为最小工序，当时任选了4号。如果选了5号结果有如何呢？见下表。

本例不同排序方案的最大流程计算

工件号	2	5	4	1	6	3
第1工序M1	2/2	4/6	4/10	6/16	5/21	9/30
第2工序M2	3/5	8/14	5/19	8/27	4/31	3/34

根据上面两表的计算结果，说明对于条件等价的条件，任选其中之一，不影响最后结果。按约翰逊法所排出的结果应为最优解，这里说明最优解可能不止一个，可以有多个等值的最优解。

约翰逊法只适用于两工序工件的排序问题，所以它的使用范围受到很大的限制。