猎鹿博弈又称猎鹿模型(Stag Hunt Model)、猎人的帕累托效率，源自启蒙思想家卢梭的著作《论人类不平等的起源和基础》中的一个故事。

古代的村庄有两个猎人。当地的猎物主要有两种：鹿和兔子。如果一个猎人单兵优作战，一天最多只能打到4只兔子。只有两个一起去才能猎获一只鹿。从填饱肚子的角度来说，4只兔子能保证一个人4天不挨饿，而一只鹿却能让两个人吃上10天。这样两个人的行为决策可以形成两个博弈结局：分别打兔子，每人得4；合作，每人得10。这样猎鹿博弈有两个纳什均衡点，那就是：要么分别打兔子，每人吃饱4天；要么合作，每人吃饱10天。

这里不妨假设两个猎人叫A和B。我们引入一种矩阵式的对两人博弈的描述方法，见下图：

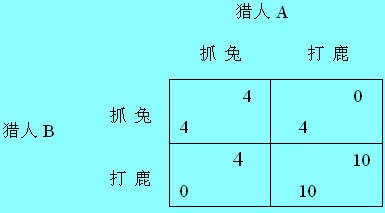
在这个矩阵图中，每一个格子都代表一种博弈的结果。具体说来，在左上角的格子表示，猎人A和B都抓兔子，结果是猎人A和B都能吃饱4天；在左下角的格子表示，猎人A抓兔子，猎人B打鹿，结果是猎人A可以吃饱4天，B则一无所获；在右上角，猎人A打鹿，猎人B抓兔子，结果是猎人A一无所获，猎人B可以吃饱4天；在右下角，猎人A和B合作抓捕鹿，结果是两人平分猎物，都可以吃饱10天。

显然，两个人合作猎鹿的好处比各自打兔子的好处要大得多，但是要求两个猎人的能力和贡献相等。如果一个猎人的能力强、贡献大，他就会要求得到较大的一份，这可能会让另一个猎人觉得利益受损而不愿意合作。“合则双赢”的道理大家都懂，在实际中很难合作的原因就在于此。合作要求博弈双方学会与对手共赢，充分照顾到合作者的利益。

在猎鹿博弈中，根据纳什均衡的定义，应用博弈论中的“严格劣势删除法”可以得到该博弈有两个纳什均衡点，那就是：要么分别打兔子，每人吃饱4天；要么合作，每人吃饱10天。

两个纳什均衡，就是两个可能的结局。两种结局到底哪一个最终发生，这无法用纳什均衡本身来确定。比较[10，10]和[4，4]两个纳什均衡，明显的事实是，两人一起去猎鹿比各自去抓兔子可以让每个人多吃12天。按照经济学的说法，合作猎鹿的纳什均衡，分头抓打兔子的纳什均衡，具有帕累托优势。与[4，4]相比，[10，10]不仅有整体福利改进，而且每个人都得到福利改进。换一种更加严密的说法就是，[10，10]与[4，4]相比，其中一方收益增大，而其它各方的境况都不受损害。这就是[10，10]对于[4，4]具有帕累托优势的含义。

在经济学中，帕累托效率准则是：经济的效率体现于配置社会资源以改善人们的境况，主要看资源是否已经被充分利用。如果资源已经被充分利用，要想再改善我就必须损害你或别的什么人，要想再改善你就必须损害另外某个人，一句话，要想再改善任何人都必须损害别的人了，这时候就说一个经济已经实现了帕累托效率。相反，如果还可以在不损害别人的情况下改善任何人，就认为经济资源尚未充分利用，就不能说已经达到帕累托效率。

目前在世界上比比皆是的企业强强联合就很接近于猎鹿博弈的帕累托改善，跨国汽车公司的联合、日本两大银行的联合等等均属此列，这种强强联合造成的结果是资金雄厚、生产技术先进、在世界上占有的竞争地位更优越，发挥的影响更显赫。总之，他们将蛋糕做得更大，双方的效益也就越高。比如宝山钢铁公司与上海钢铁集团强强联合也好，最重要的就是将蛋糕做大。在宝钢与上钢的强强联合中，宝钢有着资金、效益、管理水平、规模等各方面的优势，上钢也有着生产技术与经验的优势。两个公司实施强强联合，充分发挥各方的优势，发掘更多更大的潜力，形成一个更大更有力的拳头，将蛋糕做得比原先两个蛋糕之和还要大。

猎鹿博弈的讨论，我们的思路实际只停留在考虑整体效率最高这个角度，而没有考虑蛋糕做大之后的分配。猎鹿博弈是假设猎人双方平均分配猎物。

不妨做这样一种假设，猎人A比猎人B狩猎的能力水平要略高一筹，但B猎人却是酋长的之子，拥有较高的分配权。可以设想，A猎人与B猎人合作猎鹿之后的分配不是两人平分成果，而是A猎人仅分到了够吃2天的鹿肉，B猎人却分到了够吃18天的鹿肉。在这种情况下，整体效率虽然提高，但却不是帕累托改善，因为整体的改善反而伤害到猎人A的利益。我们假想，具有特权的猎人B会通过各种手段方法让猎人A乖乖就范。但是猎人A的狩猎热情遭到伤害，这必然会导致整体效率的下降。进一步推测，如果不是两个人进行狩猎，而是多人狩猎博弈，根据分配可以分成既得利益集团与弱势群体，这和我国的现状非常相似。