1.什么是泊松分布
Poisson分布(法语:loi de Poisson,英语:Poisson distribution,译名有泊松分布、普阿松分布、卜瓦松分布、布瓦松分布、布阿松分布、波以松分布、卜氏分配等),是一种统计与概率学里常见到的离散机率分布(discrete probability distribution),由法国数学家西莫恩·德尼·泊松(Siméon-Denis Poisson)在1838年时发表。
泊松分布的概率质量函数为:
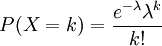
泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生率。
泊松分布适合于描述单位时间内随机事件发生的次数。如某一服务设施在一定时间内到达的人数,电话交换机接到呼叫的次数,汽车站台的候客人数,机器出现的故障数,自然灾害发生的次数等等。
若随机变量X取0和一切正整数值,在n次独立试验中出现的次数x恰为k次的概率P(X=k)=(k=0,1,...,n),式中λ是一个大于0的参数,此概率分布称为泊松分布。它的期望值为E(x)=np,方差为D(x) = λ。当n很大,且在一次试验中出现的概率P很小时,泊松分布近似二项分布。
2.泊松分布使用范围
Poisson分布主要用于描述在单位时间(空间)中稀有事件的发生数. 即需满足以下四个条件:[1]
1.给定区域内的特定事件产生的次数,可以是根据时间,长度,面积来定义;
2.各段相等区域内的特定事件产生的概率是一样的;
3.各区域内,事件发生的概率是相互独立的;
4.当给定区域变得非常小时,两次以上事件发生的概率趋向于0。 例如:
1.放射性物质在单位时间内的放射次数;
2.在单位容积充分摇匀的水中的细菌数;
3.野外单位空间中的某种昆虫数等。
3.泊松分布的期望和方差
由泊松分布知E[N(t) − N(t0)] = D[N(t) − N(t0)] = λ(t − t0)
特别的,令t_0=0.由于假设N(0)=0,故可推知泊松过程的均值函数和方差函数分别为E[N(t)] = λt,D[N(t)] = λt,
泊松过程的强度lambda (常数)等于单位长时间间隔内出现的质点数目的期望值。即对泊松分布有:E(X) = D(X) = λ
4.Poisson分布的性质
5.泊松分布的特征
1、泊松分布是一种描述和分析稀有事件的概率分布。要观察到这类事件,样本含量n必须很大。
2、λ是泊松分布所依赖的唯一参数。λ值愈小,分布愈偏倚,随着λ的增大,分布趋于对称。
3、当λ = 20时,分布泊松接近于正态分布;当λ = 50时,可以认为泊松分布呈正态分布。在实际工作中,当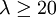 时就可以用正态分布来近似地处理泊松分布的问题。
时就可以用正态分布来近似地处理泊松分布的问题。