变量数列全称为“变量分配数列”，变量数列就是按照数量标志进行分组所形成的分配数列。例如，表1中的分配数列，则是按照年龄这个数量标志来进行分组的，所以把它叫做变量数列。

变量数列也是由两部分所组成，即：一部分是由变量值所形成的各个组，另一部分是由总体单位在各组中分配的次数所组成。而各组职工人数所占的比重，就是频率。

变量数列分为单项式变量数列和组距式变量数列，也可简称为单项数列和组距数列。

1、单项变量数列

单项变量数列，是指在变量数列中的每一个组，只用一个变量值来表示所形成的数列。见下表：

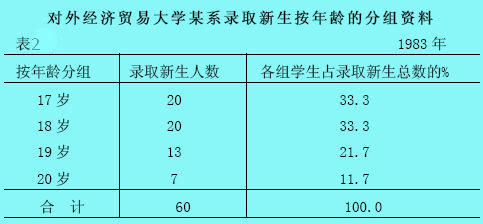
但单项变量数列的应用，受到一定的限制，一般仅适用于数列变异幅度不太大的情况；如果数列的变异范围很大，就要采用组距数列。

2、组距数列

组距数列，是指在变量数列中的每一个组，并不是由一个变量值来表示，而是由表明一定变动范围或表示一定距离的两个变量值所形成的数列。见下表：

上表中的变量数列，是一个组距数列。我们把各组的最大值称为上限，最小值称为下限，而把上限与下限之差称为组距（组中值）=（下限+上限）/2。因为，在这个数列中，每一个组的组距是10，所以又把它叫做等距数列。组距数列，可以是等距的，也可以是不等距的。我们把不等距的数列，叫做异距数列。例如，下表中的这个数列，就是一个异距数列：

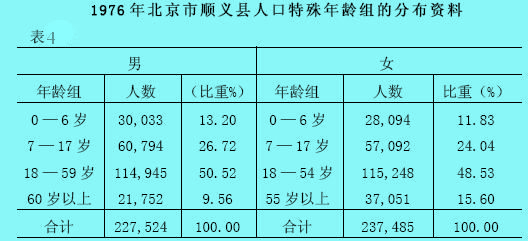
上表中的组距数列，各个组的组距都不相等，是一个比较特殊的异距数列，它是根据各个不同年龄组的特点来编制的。

关于编制变量数列，还有以下各点需要说明：

1、变量有连续变量与非连续变量之分。所谓连续变量，就是在一个变量数列中，相邻的两个变量值都是连续不断的，如产值、产量、贸易额等，都可以用小数来表示的变量；所谓非连续变量，就是在一个变量数列中，相邻的两个变量值都是可以间断的，如职工人数、工厂数、商店数、机器台数等，这些变量都只能用整数来表示。

用连续变量来编制的组距数列，不论是等距数列，还是异距数列，上一组的下限与相邻下一组的上限可以重合。如表1 和表3都属于这种情况，而且各组的排列由小到大，并把处于上下两组交界线上的变量值，都划归下一组；用非连续变量来编制的组距数列，也不论是等距数列，还是异距数列，相邻两组的上限与下限都不重合，如企业按职工人数分组，可分为100 人以下，101—500 人，501—1,000 人，1,001 人以上各组，等等。在实际工作中，为了简便起见，无论变量是否连续，常常是按连续变量分组的办法来处理的，即允许上一组的下限与下一组的上限重合。

2、在组距数列中，凡出现“以下”、“以上”字样的组叫开口组，这样的变量数列就叫做开口式数列。开口组的组距如何确定？习惯上是以相邻组的组距为组距。例如，表1中，50 岁以上这一组为开口组，相邻的一组是40—50 岁，组距是10，因此50 岁以上这一组的组距可视为10，其组中值为55[=（50+60）/2）]。

3、在编制异距数列时，组数和组距应根据现象的特点来确定；而在编制等距数列时，便要经常编制组距为5或10的等距数列。这时，确定组数和组距的经验作法是：将总体单位某一数量标志的最大值减去最小值算出全距，然后除以10或5，即可算出组数和组距来。例如，某外贸企业有职工300人，最高的工资为106元，最低的工资为30元，其全距为76，假如每隔10为一组，则可算出组数为8组，于是将全部职工人数分在30—40，40—50，⋯100—110 等八个组中去，便可编制出以组距为10的等距数列。