中位数是指将数据按大小顺序排列起来，形成一个数列，居于数列中间位置的那个数据。中位数用Me表示。

从中位数的定义可知，所研究的数据中有一半小于中位数，一半大于中位数。中位数的作用与算术平均数相近，也是作为所研究数据的代表值。在一个等差数列或一个正态分布数列中，中位数就等于算术平均数。

在数列中出现了极端变量值的情况下，用中位数作为代表值要比用算术平均数更好，因为中位数不受极端变量值的影响；如果研究目的就是为了反映中间水平，当然也应该用中位数。在统计数据的处理和分析时，可结合使用中位数。

1、中位数是以它在所有标志值中所处的位置确定的全体单位标志值的代表值，不受分布数列的极大或极小值影响，从而在一定程度上提高了中位数对分布数列的代表性。

2、有些离散型变量的单项式数列，当次数分布偏态时，中位数的代表性会受到影响。

3、缺乏敏感性。

确定中位数，必须将总体各单位的标志值按大小顺序排列，最好是编制出变量数列。这里有两种情况：

　　1、对于未分组的原始资料，首先必须将标志值按大小排序。设排序的结果为：

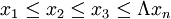
　　则中位数就可以按下面的方式确定：

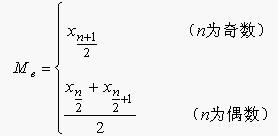
　　例如，根据下表的数据，计算50名工人日加工零件数的中位数。

　　中位数的位置在（50+1）/2 = 25.5，中位数在第25个数值（123）和第26个数值（123）之间，即Me = (123+123)/2=123(件)。

　　2、由分组资料确定中位数

　　由组距数列确定中位数，应先按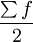的公式求出中位数所在组的位置，然后再按下限公式或上限公式确定中位数。

　　下限公式：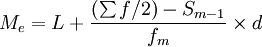

　　上限公式：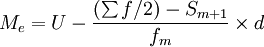

　　式中：

• M_e——中位数；

• L——中位数所在组下限；

• U——中位数所在组上限；

• f_m——为中位数所在组的次数；

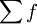• ——总次数；

• d——中位数所在组的组距；

• S_{m − 1}——中位数所在组以下的累计次数；

• S_{m + 1}——中位数所在组以上的累计次数。

　　例：根据上面例表的数据，计算50名工人日加工零件数的中位数。

　　解（某企业50名工人加工零件中位数计算表）：

　　由上表可知，中位数的位置=50/2=25，即中位数在120～125这一组，L=120，S_{m − 1} = 16，U=125，S_{m + 1} = 20，f_m = 14，d=5，根据中位数公式得：

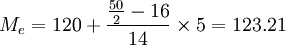　　(件)

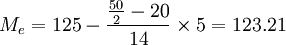　　或(件)