1.什么是节省法[1]
克拉克(Clarke)与怀特(Wright)于1964年提出该方法以求解车辆巡回问题,其思想在于按节省值(较短路径与原路径之差)由大至小排序,在车辆容量限制下,依序将对应的两顾客点排入路径中,直至所有顾客都被排入路径为止。该方法的实质要求就是节省路线成本。
Solomon于1983年将此法应用于求解时间窗约束的车辆巡回问题,关键在于当节省值较大的两顾客点被排入路径时,除需考虑车辆容量限制外,更需要考虑到时间窗的限制,也就是时间窗上界较早者,应优先被配送,并检验其时间可行性,此方法的优点是提高车辆的利用率,而两节点间的节省值的计算公式与意义如下所示:
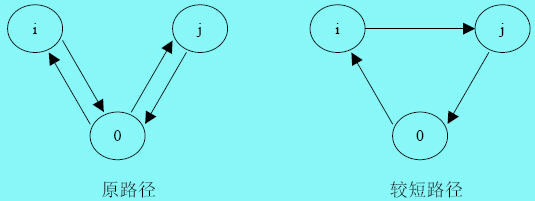
s(i,j)= d(i,0)+ d(0,j)− d(i,j)
其中d(i,0)代表顾客i至场站的距离,d(i,j)则代表顾客i至j的距离。计算两节点i与j间的节省值s(i,j)时,应先计算原路径中各往返路径的总和,再以之与较短路的总路径和相比较;两节点的原路径与较短路,如下图所示: