正态分布曲线反映了随机变量的分布规律。理论上的正态分布曲线是一条中间高，两端逐渐下降且完全对称的钟形曲线。

正态分布曲线具有以下几个方面的主要特性。

1.正态分布曲线是中间高、两边低、而且对称的光滑曲线，曲线的最高瞄在平均数处，越是接近平均数的组，变量分布的次数越多，离平均数越远，分布的次数越少。

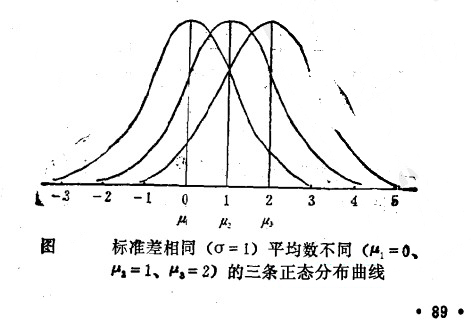
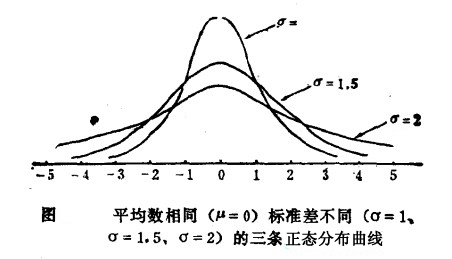
2.正态分布曲线因总体平均数和标冶差的不同呈现为不同的曲线，所以它不是一条曲线，而是一个曲线系统，不同的总体都有它自己的曲线。下两图表示平均数和标混差不同的正态分布曲线。

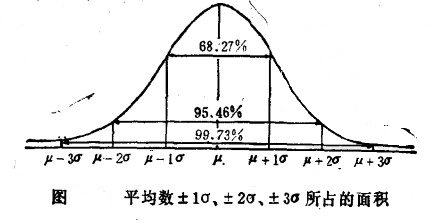
3.正态分布曲线与横轴间的总面积作为1，由平均数的两侧各距1个标准差的距离，与横轴作两条垂直线，两条垂直线内的面积约占曲线内总面积的68.2796；从平均数的商测各距2个标准差的距离作两条垂直线，则所占面积为95.46%，取3个标准差，则占99.73%，如图所示。上述一定区间的面积占总面积的百分率，意味着总体的变数在此区间内分布的概率。

上述一定区间变数的理论分布概率，可以从实际调查的资料加以验证。现以水稻杂交种“南优2号”100株株高的样本资料，在overline{X}土1s土2s、土3s三个范国内观察值的分布次数统计如表。

水稻杂交种“南优2号”100株株高的样本资料，在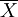土1s土2s、土3s三个范国内观察值的分布次数

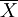±ks	数值	范围	范围内观察值次数	理论次数
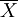±1s	94.18±3.61	90.57-97.79	72	68.27
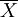±2s	94.18±7.22	86.96-101.40	94	95.46
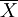±2s	94.18±10.83	83.35-105.01	100	99.73