1.什么是期望值法
2.期望值法的步骤
采用期望值法进行概率分析,一般需要遵循以下步骤:
1、选用净现值作为分析对象,并分析选定与之有关的主要不确定性因素。
2、按照穷举互斥原则,确定各不确定性因素可能发生的状态或变化范围。
3、分别估算各不确定性因素每种情况下发生的概率。各不确定性因素在每种情况下的概率,必须小于等于1、大于等于零,且所有可能发生情况的概率之和必须等于l。这里的概率为主观概率,是在充分掌握有关资料基础之上,由专家学者依据其自己的知识、经验经系统分析之后,主观判断作出的。
4、分别计算各可能发生情况下的净现值(NPV)。各年净现值期望值、整个项目寿命周期净现值的期望值、各年净现值期望值的计算公式为:
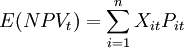
式中,E(NPVt)为第t年净现值期望值;Xit为第t年第i种情况下的净现值;Pit为第t年第i种情况发生的概率,n为发生的状态或变化范围数。
整个项目寿命周期净现值的期望值的计算公式为:
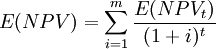
式中,E(NPV)为整个项目寿命周期净现值的期望值;i为折旧率;M为项目寿命周期长度,E(NPVT)为第t年净现值的期望值。
项目净现值期望值大于零,则项目可行,否则,不可行。
5、计算各年净现值标准差、整个项目寿命周期净现值的标准差或标准差系数,各年净现值标准差的计算公式为:
![delta_t=sqrt{sum_{i=1}^n[X_{it}-E(NPV_t)]^2P_{it}}](/uploads/2015/03/69101426155469.png)
式中,δt为第t年净现值的标准差,其它符号意义同前。
整个项目寿命周期的标准差计算公式为:
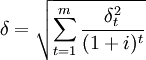
式中,δ为整个项目寿命周期的标准差。
净现值标准差反映每年各种情况下净现值的离散程度和整个项目寿命周期各年净现值的离散程度,在一定的程度上,能够说明项目风险的大小。但由于净现值标准差的大小受净现值期望值影响甚大,两者基本上呈同方向变动。因此,单纯以净现值标准差大小衡量项目风险性高低,有时会得出不正确的结论。为此需要消除净现值期望值大小的影响,利用下式计算整个项目寿命周期的标准差系数:
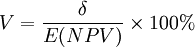
式中,V为标准差系数。一般地,V越小,项目的相对风险就越小,反之,项目的相对风险就越大。依据净现值期望值、净现值标准差和标准差系数,可以用来选择投资方案。判断投资方案优劣的标准是:期望值相同、标准差小的方案为优;标准差相同、期望值大的方案为优;标准差系数小的方案为优。
6、计算净现值大于或等于零时的累计概率。累计概率值越大,项目所承担的风险就越小。
7、对以上分析结果作综合评价,说明项目是否可行及承担风险性大小。
3.期望值法应用示例[1]
【例】某投资者以25万元购买了一个商铺单位2年的经营权,第一年净现金流量可能为:22万元、18万元和14万元,概率分别为0.2、0.6和o.2;第二年净现金流量可能为:28万元、22万元和16万元,概率分别为O.15、0.7和0.15,若折现率为10%,问该购买商铺的投资是否可行。
【解】
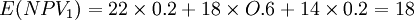 (万元)
(万元)
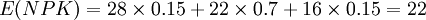 (万元)
(万元)
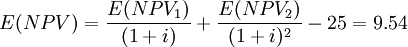 (万元)
(万元)
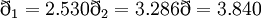
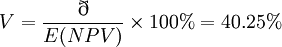
因此,该投资项目可行,且风险较小。
【例】某项目投资20万元,建设期1年。据预测,经营期内的年收入可能为5、10、12.5万元,相应的概率为0.3、O.5和0.2。同时,预计受技术进步的影响,经营期可能为2、3、4、5年,对应的可能性为0.2、0.2、0.5和0.1。如果折现率为10%,对净现值作累计概率分析。
【解】以年收入为10万元,经营期4年为例。该投资项目的净现值为:
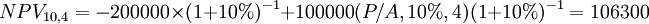 (元)。
(元)。
其他各种情况下的净现值如图所示。
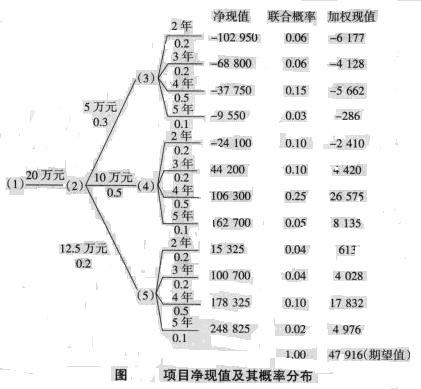
可以计算得出,该投资项目的净现值期望值为47916元,净现值大于零的累计概率P(NPV>0)为0.6.表明该项目可行。