平均数-管理百科

1.什么是平均数

平均数是统计学中最常用的统计量，用来表明资料中各观测值相对集中较多的中心位置。在畜牧业、水产业生产实践和科学研究中，平均数被广泛用来描述或比较各种技术措施的效果、畜禽某些数量性状的指标等等。

统计平均数是用于反映现象总体的一般水平，或分布的集中趋势。数值平均数是总体标志总量对比总体单位数而计算的。^[1]

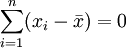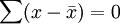
　　 $sum_{i=1}^n(x_i-bar{x})=0$ 或简写成 $sum(x-bar{x})=0$

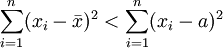　　 $sum_{i=1}^n(x_i-bar{x})^2<sum_{i=1}^n(x_i- a)^2$ 　　　　（常数a≠ $bar{x}$ ）

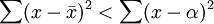
　　或简写为： $sum(x-bar{x})^2<sum(x-alpha)^2$

　　以上两个性质可用代数方法予以证明。

　　对于总体而言，通常用μ表示总体平均数，有限总体的平均数为：

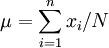
　　 $mu=sum_{i=1}^nx_i/N$

　　式中，N表示总体所包含的个体数。

　　当一个统计量的数学期望等于所估计的总体参数时，则称此统计量为该总体参数的无偏估计量。统计学中常用样本平均数（ $bar{x}$ ）作为总体平均数（μ）的估计量，并已证明样本平均数是总体平均数μ的无偏估计量。

　　平均数主要包括有算术平均数（arithmetic mean）、中位数（median）、众数（mode）、几何平均数（geometric mean）及调和平均数（harmonic mean）。

　　1、算术平均数（arithmetic mean）

　　算术平均数是指资料中各观测值的总和除以观测值个数所得的商，简称平均数或均数，记为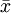 $bar{x}$ 。

　　2、中位数（median）

　　中位数是指将数据按大小顺序排列起来，形成一个数列，居于数列中间位置的那个数据。中位数用Me表示。

　　从中位数的定义可知，所研究的数据中有一半小于中位数，一半大于中位数。中位数的作用与算术平均数相近，也是作为所研究数据的代表值。在一个等差数列或一个正态分布数列中，中位数就等于算术平均数。

　　在数列中出现了极端变量值的情况下，用中位数作为代表值要比用算术平均数更好，因为中位数不受极端变量值的影响；如果研究目的就是为了反映中间水平，当然也应该用中位数。在统计数据的处理和分析时，可结合使用中位数。

　　3、众数（mode）

　　众数是指一组数据中出现次数最多的那个数据，一组数据可以有多个众数，也可以没有众数。

　　4、几何平均数（geometric mean）

　　几何平均数是n个变量值连乘积的n次方根。

　　几何平均数多用于计算平均比率和平均速度。如：平均利率、平均发展速度、平均合格率等。

　　5、调和平均数（harmonic mean）

　　调和平均数又称倒数平均数，是变量倒数的算术平均数的倒数。