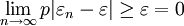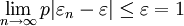1.什么是大数定律
大数定律是指在随机试验中,每次出现的结果不同,但是大量重复试验出现的结果的平均值却几乎总是接近于某个确定的值。
其原因是,在大量的观察试验中,个别的、偶然的因素影响而产生的差异将会相互抵消,从而使现象的必然规律性显示出来。例如,观察个别或少数家庭的婴儿出生情况,发现有的生男,有的生女,没有一定的规律性,但是通过大量的观察就会发现,男婴和女婴占婴儿总数的比重均会趋于50%。
2.大数定律的表现形式
定义1:设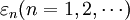 为概率空间(Ω,F,P)上定义的随机变量序列(简称随机序列),若存在随机变数
为概率空间(Ω,F,P)上定义的随机变量序列(简称随机序列),若存在随机变数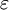 ,使对任意
,使对任意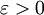 ,恒有:
,恒有:
则称随机序列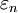 依概率收敛于随机变量
依概率收敛于随机变量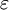 (
(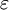 也可以是一个常数),并用下面的符号表示:
也可以是一个常数),并用下面的符号表示:
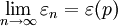 或
或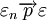
定义2:设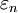 为一随机序列,数学期望
为一随机序列,数学期望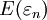 )存在,令
)存在,令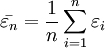 ,若
,若![lim_{ntoinfty}[bar{varepsilon_n}-E(bar{varepsilon_n})]=](http://wiki.mbalib.com/w/images/math/b/f/a/bfaf433f620b60488d833822bad07e84.png) 0(P),则称随机序列
0(P),则称随机序列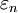 服从大数定律,或者说大数法则成立。
服从大数定律,或者说大数法则成立。
定义3:设Fn(x)是分布函数序列,若存在一个非降函数F(x),对于它的每一连续点x,都有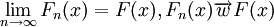 ,则称分布函数序列Fn(x)弱收敛于F(x)。
,则称分布函数序列Fn(x)弱收敛于F(x)。
定义4:设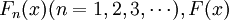 分别是随机变量
分别是随机变量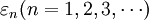 及
及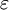 的分布函数,若
的分布函数,若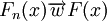 ,则称
,则称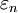 依分布收敛于
依分布收敛于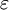 ,亦记为
,亦记为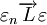 ,且有:(1)若
,且有:(1)若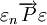 ,则
,则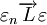 ;(2)设c为常数,则
;(2)设c为常数,则 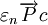 的充要条件是
的充要条件是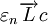 。
。
逆极限定理:设特征函数列fn(t)收敛于某一函数f(t),且f(t)在t=0时连续,则相应的分布函数列Fn(x)弱收敛于某一分布函数F(x),而且f(t)是F(x)的特征函数。
大数定律有若干个表现形式。这里仅介绍其中常用的两个重要定律:
(一)切贝雪夫大数定理
设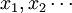 是一列两两相互独立的随机变量,服从同一分布,且存在有限的数学期望a和方差σ2,则对任意小的正数ε,有:
是一列两两相互独立的随机变量,服从同一分布,且存在有限的数学期望a和方差σ2,则对任意小的正数ε,有:
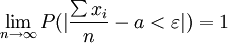
该定律的含义是:当n很大,服从同一分布的随机变量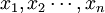 的算术平均数
的算术平均数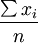 将依概率接近于这些随机变量的数学期望。
将依概率接近于这些随机变量的数学期望。
将该定律应用于抽样调查,就会有如下结论:随着样本容量n的增加,样本平均数将接近于总体平均数。从而为统计推断中依据样本平均数估计总体平均数提供了理论依据。
(二)贝努里大数定律
设μn是n次独立试验中事件A发生的次数,且事件A在每次试验中发生的概率为P,则对任意正数ε,有:
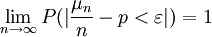
该定律是切贝雪夫大数定律的特例,其含义是,当n足够大时,事件A出现的频率将几乎接近于其发生的概率,即频率的稳定性。
在抽样调查中,用样本成数去估计总体成数,其理论依据即在于此。