1.什么是分期付款

分期付款(Pay by Instalments)是购买商品和劳务的一种付款方式。大多用在一些生产周期长、成本费用高的产品交易上。如成套设备、大型交通工具、重型机械设备等产品的出口。
2.分期付款的发展
分期付款方式是在第二次世界大战以后发展起来的。开始时只局限于一般日用商品或劳务的购买。后来,随着生产力的迅速发展,工、农业生产的规模日益扩大,所需费用增大,加之银行信用的发展,分期付款的领域扩大到企业购买大型机器设备和原材料上。
近年来伴随着中国金融服务的完善以及人们消费习惯的改变,在国外流行的分期付款消费被引入国内,并迅速得到国内消费者的认可。采用分期付款方式消费的通常是目前支付能力较差,但有消费需求的年轻人。其消费的产品通常是笔记本电脑、手机、数码产品等。
3.分期付款的特点
分期付款的做法是在进出口合同签订后,进口人先交付一小部分货款作为订金给出口人,其余大部分货款在产品部分或全部生产完毕装船付运后,或在货到安装、试车、投入以及质量保证期满时分期偿付。
分期付款实际上是卖方向买方提供的一种贷款,卖方是债权人,买方是债务人。买方在只支付一小部分货款后就可以获得所需的商品或劳务,但是因为以后的分期付款中包括有利息,所以用分期付款方式购买同一商品或劳务,所支付的金额要比一次性支付的货款多一些。
买卖双方在成交时签订契约,买方对所购买的商品和劳务在一定时期内分期向卖方交付货款。每次交付货款的日期和金额均事先在契约中写明。
4.分期付款方式
分期付款方式通常由银行和分期付款供应商联合提供。
银行为消费者提供相当于所购物品金额的个人消费贷款,消费者用贷款向供应商支付货款,
同时供应商为消费者提供担保,承担不可撤消的债务连带责任。
5.分期付款的优势
一方面可以使卖方完成促销活动;
另一方面也给买方提供了便利。
6.分期付款的计算方法 [1]
在分期付款中还要了解分期付款的有关计算。
1.等额偿还方式
若年初向银行贷款D(元),准备分n期偿还,每期均偿还P(元),期利率为R。
贷款一期后,本金和应为D(1+R)。
第一次还款后剩余款项为b1 = D(1 + R) − P,由于所剩款项要付利息,故第二次还款是在(D(1+R)-P)(1+R)的基础上还P元,即第二期偿还后剩余款项为:
b2 = D(1 + R)2 − P(1 + R) − P
如此类推,第n期期末还P元便立即结算(不涉及复利)
故有:![b_n=D(1+R)^n-P[(1+R)^{n-1}+(1+R)^{n-2}+cdotscdots+1]=0](http://wiki.mbalib.com/w/images/math/7/0/0/700973cd33188674f4221d6cdaa4c0a4.png)
即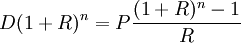
从而每期应偿还的数目为
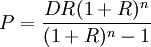
2.不等额偿还
如果不是每期都偿还P元,而是第一期还P1,第二期还P2, …第n期还Pn后,便立即结算。
则:第一期偿还后,还剩:
D(1 + R)n − P1
第二期偿还后,还剩:
[D(1 + R)2 − P1](1 + R) − P2 = D(1 + R)2 − P1(1 + R) − P2
第三期偿还后,还剩:
[D(1 + R)2 − P1(1 + R) − P2](1 + R) − P3 = D(1 + R)3 − P1(1 + R)2 − P2(1 + R) − P3
由此类推,第n期偿还Pn后,便还清所有款项即:
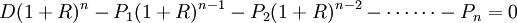
即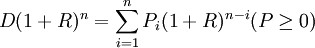
3.应用(等额方式)
某用户从21岁开始,每年存入银行退休保险金a元,如果平均每年利息为R,直到60岁退休为止,从61岁开始每年从银行提取2万元,预计能连续支付40年,则该用户在工作期间,每年存入银行的钱款数为多少?解:第一年(21岁时)存入a元,当此用户61岁去取时,a元就会升值到
a(1 + R)40
第二年又存入a元,最终升值到a(1 + R)39
由此得出数列an
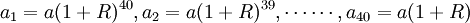
则有![S_{40}=a_1+a_2+cdotscdots+a_{40}=a(1+R)[(1+R)^{39}+(1+R)^{38}+cdotscdots+1]=a(1+R)frac{(1+R)^{40}-1}{R}](http://wiki.mbalib.com/w/images/math/4/d/7/4d7c20e5c3ca9287c9e1bfced16c02da.png)
此用户61岁开始逐年提取退休保险金。
第一年取2万元,那么还剩(S40 − 2)万元;
第二年取2万元,因为前一年取剩的钱还有利息,所以第二年取剩的钱就为(S40 − 2)(1 + R) − 2
由此可得数列:bn
b1 = S40 − 2
b2 = (S40 − 2)(1 + R) − 2
b3 = (S40 − 2)(1 + R)2 − 2(1 + R) − 2
…………
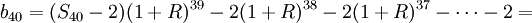
![S_{40}(1+R)^{39}-2(1+R)^{38}-2(1+R)^{37}-cdots-2=S_{40}(1+R)^{39}-2[(1+R)^{38}+(1+R)^{37}+cdots+1]=s_{40}(1+R)^{39}-frac{(1+R)^{40}-1}{R}=0](http://wiki.mbalib.com/w/images/math/6/1/6/6163224c363bb51ebb2ef54cd3da0d0b.png)
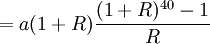 ①
①
又![S_{40}(1+R)^{39}=frac{2[(1+R)^{4}-1]}{R}](http://wiki.mbalib.com/w/images/math/3/f/6/3f6a527d40ffe7d7b9f8296ef56f41e6.png) ②
②
由①②得![a(1+R)frac{(1+R)^{40}-1}{R}(1+R)^{39}=frac{2[(1+R)^{4}-1]}{R}](http://wiki.mbalib.com/w/images/math/a/c/c/acc1c9c73a2597386b1d729304b6f670.png)
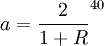
故每年应向银行存入元才能保证退休后每年能取2万元钱而取整整40年。
7.延期付款与分期付款的区别[2]
延期付款虽与分期付款类似,但两者还是有下列重大区别。
(1)货款支付时问不同。采用分期付款,其货款是在交货时付清或基本付清;而采用延期付款时,大部分货款是在交货后一个相当长的时间内分期摊付。
(2)货物所有权转移时间不同。采用分期付款时,只要付清最后一笔货款,货物所有权即行转移;而采用延期付款时,货物所有权一般在交货时即转移。
(3)是否要求买方向卖方支付利息问题上也有所不同。采用分期付款,买方没有利用卖方的资金,因而不存在利息问题;而采用延期付款时,买方利用了卖方的资金需要向卖方支付利息。
在采用分期付款或延期付款时往往将汇付、托收和信用证付款三者结合使用,即主要货款采取信用证付款方式,少量货款或货款尾数则采用汇付或托收方式。